Names Of Different Quadrilaterals – We learned about different forms. Let’s watch this video to learn about this shape and what we call it.

All sides or corners of the door are straight. You can see more of these objects around you. Some of them are listed below.

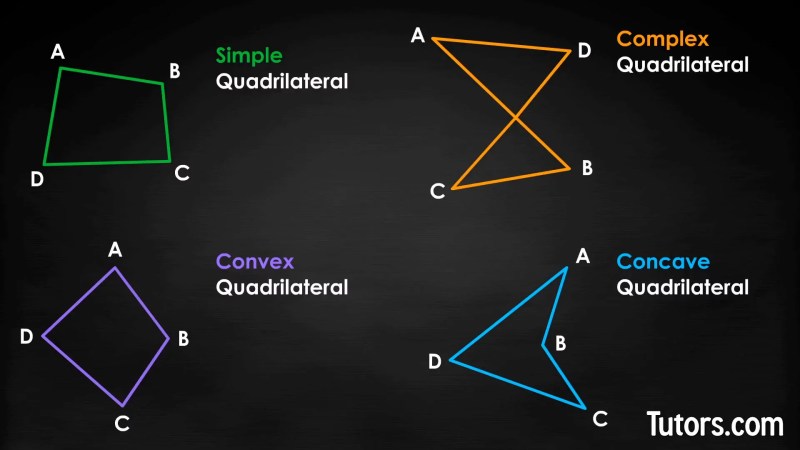
Names Of Different Quadrilaterals

Each of these figures is made up of segments. To use these shapes in a building or other real-world structure, it’s important to know:

D And 3d Shapes: Definition, Properties, Formulas, Types Of 3d Shapes

We all know that many objects we use in real life are square. Each side was a segment. These shapes are called quadrilaterals.

A quadrilateral is a closed geometric figure made up of four segments called sides.

We learned about the properties of polygons. So you need to check these properties to identify polygons. A figure is a polygon if a given figure has all properties. Properties identified in this figure:

The polygon with the smallest number of sides (that is, three sides) is called a triangle. Similarly, polygons with different numbers of sides have different names.

How To Memorize The Properties Of Quadrilaterals

Do you know why a polygon with three sides is called a triangle? The word “three” means three. So a triangle means three angles. A polygon with three sides is called a triangle because it has three angles.

In general, a polygon with n sides is called an n-gon. A prefix is ​​a Greek word for a specific number. For example, “penta” is a Greek word meaning “five”. Therefore, a polygon with 5 sides/edges is called a pentagon.

You can see that each pair of polygon sides intersect at a point. This point is called the vertex of the polygon. In any polygon, the number of vertices is equal to the number of sides of the polygon. Let’s name the vertices of the polygon above.

Here all 4-line segments are drawn from one vertex A to another vertex of the polygon. However, two of them are sides of the polygon and the other two are not. How do you tell them apart?

What Is A Quadrilateral? (definition, Properties & Shapes) // Tutors.com

The figure shows that vertices B and E are adjacent (continuous) to vertex A. However, vertices C and D are not adjacent to vertex A. Thus, each side of the polygon connects two consecutive vertices of the polygon. . So what do we call a segment connecting two non-contiguous vertices?

A polygon’s diagonals connect only non-contiguous vertices of the polygon. Each line segment connecting two non-contiguous vertices of a polygon is a diagonal.

You can draw 3 diagonals from each of the 6 vertices of the hexagon. But there are only 9 non-repeating diagonals.

Is there a relationship between the number of sides and the number of diagonals in a polygon? Let’s start with the rectangle.

Names Of Quadrilaterals

Consider the quadrilateral ABCD. How many peaks are there? Every rectangle has 4 sides and 4 vertices. Now consider node A.

How many vertices are there in the quadrilateral ABCD that are not adjacent to A? One vertex, vertex C. This means that it is impossible to draw a diagonal from vertex A to vertices B and D. It is also impossible to draw a diagonal to yourself from any vertex. Only vertex C can draw a diagonal from vertex A. The same goes for other vertices. You can draw only one diagonal from every vertex of a quadrilateral.

So the rectangle must have 4 diagonals. But we only found two. Why? Don’t forget that each diagonal is split into 2 vertices. Computing the same diagonal for two vertices results in twice as many diagonals as it actually is.

Of the five vertices, P and S follow T. So you can’t draw a diagonal line from T to that vertex. Also, you can’t draw diagonal lines for yourself. So you cannot draw a diagonal from T from 5 vertices to 3 vertices.

Types Of Quadrilaterals And Their Properties

The same goes for other peaks. So you can only draw 2 diagonals out of 5 vertices.

For example, the diagonal TR is calculated as the diagonal in both T and R. That is, it is counted twice. This applies to all diagonals. So 5 × (5 – 3) must be divided by 2 to get the actual score.

Of course, since a polygon has 6 sides, there is no difference in the number of sides.

The diagonal of the concave polygon seen in the previous example looks like the image below.

Figure 2 From Understanding Inclusion Relations Between Quadrilaterals

Can you tell the difference between the diagonal of a concave polygon and the diagonal of a convex polygon?

Notice that none of the diagonals of a convex polygon have a part outside the polygon.

In a concave polygon, you can see that some of the many diagonals are outside the polygon.

A polygon is said to be a regular polygon only if it is equilateral as well as equilateral. That is, a regular polygon has equal sides and angles. Two very familiar examples of regular polygons are equilateral triangles and squares.

What Are The Types Of Quadrilaterals?

We know that polygons can be classified as triangles, squares, pentagons, hexagons, etc, depending on the number of sides.

If these polygons are regular polygons, add a “regular” prefix to their name. For example, a pentagon with equal sides and angles is called a regular pentagon.

A rectangle has only two sides of equal length and each interior angle is 90°. So a rectangle is an equilateral but not equilateral side, so a rectangle is an irregular polygon.

This polygon has equal faces but not equal angles. So a concave polygon is equilateral but not equilateral. Therefore, it is an irregular polygon.

Quadrilaterals Card Sort

Now you can see that the interior angle of a polygon is divisible by the interior angle of any triangle as shown in the image below.

The sum of the interior angles of three triangles is the sum of the interior angles of a pentagon. This pentagon has 3 such triangles.

Let’s compare the number of sides/edges and the sum of the interior angles for the two polygons we discussed.

Here we also observe that the interior angle of a polygon is divided by the interior angle of a triangle. A polygon has 6 sides and is divided into 4 triangles.

Get The Knowledge Of Science

Sum of interior angles of a polygon with n sides = (n – 2) × 180°

To find the size of each interior angle of a polygon, divide the sum of the interior angles by the number of angles in the polygon.

To find the missing angle measure of a polygon with face “n” given the sum of (n – 1) angles:

The angle formed on the outside of the triangle when one side of the triangle is extended is called the exterior angle. Consider polygon ABCD. The side BC of the polygon continues to point to point E.

Nelson International Maths Workbook 4 Answers By Hany Mufeid

∠DCE is now formed on the outside of the polygon by extending the sides of the polygon. This is the exterior angle of polygon ABCD.

(You can prove it logically using the formula for sum of interior angles of a polygon.)

To find the dimension of one outer edge of a polygon when you know the dimensions of the other edge:

In a polygon, the number of sides, the number of interior angles, and the number of exterior angles are the same. So, for a regular polygon with “n” sides, the number of outer edges is also “n”.

Mars: Describing And Defining Quadrilaterals

The number of sides of a regular polygon is found by dividing 360° by the value of each exterior angle.

Now you know how to find the number of sides of a regular polygon given the exterior angles.

Using this relationship between the interior angle and its exterior angle, you can find the number of sides of a regular polygon, given the interior angle measure of the polygon, by following these steps:

How can i say For a square or rhombus, each pair of adjacent sides is equal. Therefore, it can be said that a square and a rhombus can also be a kite.

Congruent Shapes: Triangles, Quadrilaterals, Irregular Shapes And Circles • 7esl

When we need to find the length of a side of a parallelogram given the lengths of adjacent sides, we apply the following properties:

Parallelogram ABCD, AB = 6 cm, AD = 4.5 cm We can find the lengths of the other two sides BC and CD as follows.

What is the length of the diagonal? Assume that the diagonals PR and AL intersect in half at point O.

To find the length of the side of a parallelogram given the ratio between the perimeter and the side, follow these steps:

Properties Of Quadrilaterals

To find the length of a side given the ratio of the sides to the perimeter of a parallelogram, follow these steps:

To find an angle given the measurement of adjacent angles

What are the different kinds of quadrilaterals, properties of different quadrilaterals, names of quadrilaterals, names of all quadrilaterals, different quadrilaterals and their properties, different quadrilaterals, different kinds of quadrilaterals, different names of quadrilaterals, what are the different types of quadrilaterals, different type of quadrilaterals, mathematical names of quadrilaterals, properties of different types of quadrilaterals