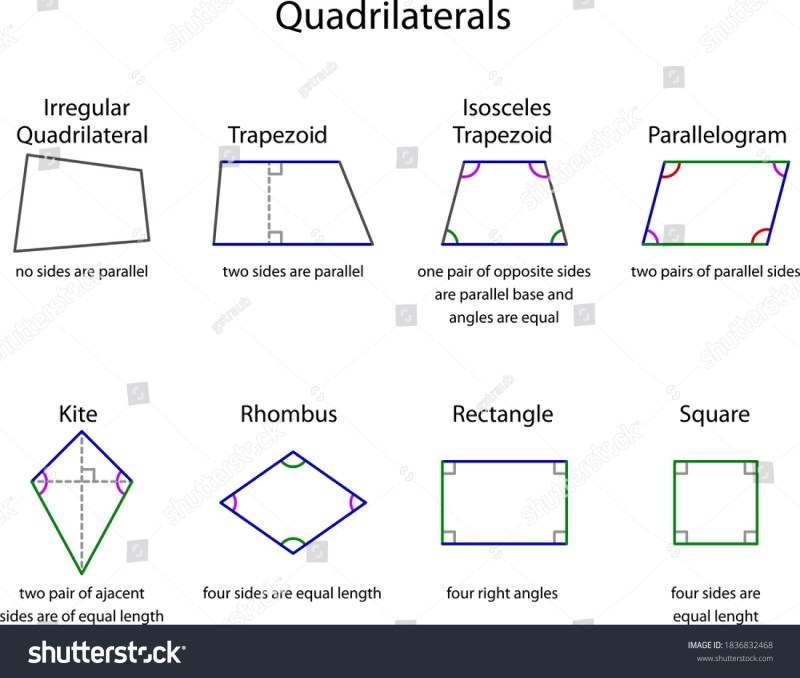
What Are The Different Types Of Quadrilaterals – The term quadrilateral comes from the terms “quad” meaning four, and “lateral” meaning side. A quadrilateral is defined as a closed two-dimensional figure, with exactly four sides and four angles. As you might expect, there are many shapes that can be made with four sides and four angles. The six most common polygons that fall under the umbrella of “quadrilateral” are: parallelograms, trapezoids, rectangles, squares, kites, and rhombuses. Let’s look at the similarities and differences between each category of quadrilateral.
Some quadrilaterals can be classified into more than one group. A flow chart can be a useful visual aid when learning which shapes belong in more than one category.
What Are The Different Types Of Quadrilaterals

Let’s start with the “parallelogram” category, which has a shape you’re probably familiar with. The square.
Types Of Quadrilaterals
A square is a quadrilateral with four equal side lengths, and four equal angles. Similarly, a rectangle is a quadrilateral with four congruent angles, and opposite side lengths of equal length. This means that a rectangle can never be classified as a square, but technically a square can be classified as a rectangle. Similarly, a square can also be classified as a red, but not all reds can be classified as a square. This is because a rhombus has four sides of equal length. However, the angular measurements do not have to match. Rectangles, rectangles, and squares all fall into the category of parallelograms because they each have two pairs of parallel sides.
A shape that is not considered a parallelogram is a trapezoid. A trapezoid has exactly one set of parallel sides. Within the trapezoid family there are isosceles trapezoids. Isosceles trapezoids have equal non-parallel sides.
The final shape under the rectangular umbrella is the kite. A kite is a quadrilateral without parallel sides.
As you can see, the term quadrilateral describes a wide range of polygons. These shapes are studied in detail in the subject of geometry. Geometry is essentially the “study of shapes,” which has many useful real-world applications. For example, engineers use geometry to evaluate the strengths and weaknesses of shapes when designing large bridges. Bridges often use triangles because of their proven strength against weight and pressure. Geometry is also used in the field of astronomy. Shapes such as elliptical orbits are studied to determine the correct angle to safely enter a planet’s atmosphere. Geometry calculations were even used in the last Mars rover landing! As you can see, the field of geometry, and specifically the study of shapes, has many useful applications in the fields of science, engineering, and mathematics.
A Lesson Plan (of Sorts) For Quadrilaterals
A quadrilateral is a two-dimensional shape, with four straight sides. Examples of quadrilaterals include parallelograms, trapezoids, rectangles, kites, squares, and rhombuses.
A rhombus is a quadrilateral with four sides of equal length. It can take the form of a square where all side lengths are equal, and all angles are 90°. However, shapes other than squares can be formed with four equal side lengths. Any shape with four sides of equal length is considered a rhombus. Therefore, a square is always a rhombus, but a rhombus is not always a square.
Aimee and Sam make a bookshelf with a trapezoid as the basic shape. The two sketch what they think a trapezoid should look like, but Aimee says that the shape Sam drew isn’t considered a trapezoid? Is he right?

Aimee says that the shape Sam drew is not considered a trapezoid, which is wrong. A trapezoid is defined as a quadrilateral with exactly one set of parallel sides. Aimee and Sam both drew quadrilaterals with exactly one set of parallel sides, so both shapes qualify as trapezoids.
Types Of Quadrilateral Worksheet
The figure is not a parallelogram because it does not have two sets of parallel sides. It is not a trapezoid because it does not have exactly one set of parallel sides. It is not a rhombus because it does not have four sides of equal length. However, it is considered a quadrilateral because it is a closed shape with four sides and four angles.
Jenny makes necklaces to sell at the farmers market. She creates necklaces with small pieces of colored stones. How should Jenny describe the flat face of the stones to her clients?
The flat face of the stone is four-sided, with exactly one set of parallel sides. This means they can be classified as trapezoids. All four-sided closed figures can be called quadrilateral. But when the sides, angles, and diagonals obey specific properties, they are quadrilaterals identified by specific names rather than just quadrilaterals.
A parallelogram is formed by connecting two congruent triangles (triangles that are congruent in all respects, be it congruent sides or angles) back to back.
Quadrilateral Images, Stock Photos & Vectors
A rectangle can be considered a parallelogram with all four angles equal. So if we arrange all the angles of a parallelogram at 90 degrees each, we get a rectangle.
A rhombus is a parallelogram with all four sides equal. So just as a parallelogram, of course all four angles are not necessarily equal, but it follows all the properties of a parallelogram. Let’s see what the additional features are.
From trying a new hobby to having sex – 20 ways to recharge and boost your mood in 2023

A trapezium differs from the quadrilaterals discussed above in that it does not have as many specifications to achieve. The only condition to form a trapezoid is that it must have a pair of parallel sides.
Properties Of All Types Of Quadrilateral And Its Diagonals
If the trapezium is considered and the vertices of the upper vertices are dropped, as shown in the figure above, the quadrilateral formed at the intersection is a rectangle, but the right triangles are needed on both sides of this rectangle not to be congruent, because their bases need not be congruent. always the same.
If the non-parallel sides of a trapezoid are equal, then the right triangle formed will be congruent and therefore have the same base. This gives the trapezium a new name: Isosceles trapezium.
We saw how we can connect rectangles, rectangles and squares with basic parallelograms and also discussed the add-on properties that make them different from parallelograms in one way or another. So it is always good to learn the properties of parallelograms and memorize the fact that rectangles are parallelograms with equal angles, rhombuses are those with equal sides and squares are a combination of all these. We also talked about trapezes and kites, which also left this group. Now just try to remember the properties, hopefully you will find it easier.
This content is accurate and correct to the best of the author’s knowledge and is not intended to replace formal, individual advice from a qualified professional.
Chart Different Types Quadrilaterals Stock Vector (royalty Free) 1836832468
Once upon a time in America When God belonged, guns on trucks were common, The Golden Rule existed, Massacres not Quadrilaterals are Polygons. They are part of a plane bounded by four sides (quad means four and lateral means side). All quadrilaterals have exactly four sides and four angles. They can be classified into specific groups based on the length of their sides or the measure of their angles.
Shapes with four sides include the square, rectangle, trapezoid, rhombus, parallelogram, and kite (also called a tangential quadrilateral). As long as the four sides are connected by straight lines, it is a quadrilateral. It does not have to form a recognizable shape.
The angles at vertices $ A, B, C$ and $ D$ are usually labeled in the order: $alpha, beta, gamma, delta$ (alpha, beta, gamma, delta).

The first group of quadrilaterals is a scalene quadrilateral. A scalene quadrilateral is a quadrilateral without special features. The sides and angles have different lengths and measures.
Teaching In Special Education: Quadrilaterals
The height or altitude of a trapezoid is the length of a line perpendicular to the base and through the opposite vertex. A trapezoid will have the same height regardless of which vertex we draw it from. If we draw a height from the larger base, we simply extend the shorter base.
If $alpha$ is an angle at vertex $A$, $beta$ at vertex $B$, $gamma$ at vertex $C$ and $delta$ at vertex $D$ in a trapezoid $ABCD$, then valid:
The height of a parallelogram, labeled $h$, is the line segment that connects a vertex to an opposite side, and is perpendicular to that side.
In addition to parallelograms that are quadrilaterals, there are several shapes that are parallelograms as well as quadrilaterals. It is a square, rectangle, and rhombus.
What Are The Types Of Quadrilaterals?
Let $ABCD$ be a parallelogram. Opposite angles in a quadrilateral $ABCD$ are congruent, and adjacent angles are supplementary.
Each of the above statements could be an alternative definition of a parallelogram. We have to prove the rest of the statements.
Since the line $AC$ is a traverse of the parallel lines $AB$ and $CD$, then $angle =angle$. The line $AC$ is also a traverse of the parallel lines $BC$ and $AD$ which is $angle=angle$.

$overline$ is also the common segment of triangles $ABC$ and $CDA$. By the A-S-A theorem of congruence of triangles, triangles $ABC$ and $CDA$ are congruent. This is followed by $|AB| = |CD]$ and $|AD| = |BC|$.
Quadrilaterals (sample Questions)
Since $AC$ is a traverse
Different types of quadrilaterals and their properties, different names of quadrilaterals, what are the quadrilaterals, what are the types of quadrilaterals, what are the different types of dialysis, different types of quadrilaterals, what are the different kinds of quadrilaterals, what are the different types of lupus, different kinds of quadrilaterals, what are the different types of eczema, properties of different quadrilaterals, properties of different types of quadrilaterals