Vertex Angle In An Isosceles Triangle – Remember that an isosceles triangle has at least two congruent sides. Articulating parts are called legs. A vertical angle is the angle formed by the legs. The opposite side of a vertical angle is called the base, and base angles are two angles with the same base. 3 is a vertical angle. 1 and 2 are primary angles. Remember the definition of an isosceles triangle: if isosceles, then at least 2 congruent (congruent?) sides.
4 Ch 6 Two related theorems: The positions of the longest and shortest sides of a triangle correspond to the positions of the largest and smallest angles. 6-9 6-10
Vertex Angle In An Isosceles Triangle

8 The following collinearity and its inverse show the relationship between an equilateral triangle and an equilateral triangle. 5-2 5-3
Copyright © Cengage Learning. All Rights Reserved.
10 Example 4A: For isosceles ∆LMP with base LM, MP = 2x + 10, PL = x + 30, LM = 4x. Find the MP
Example 4B: ∆OLD is isosceles to the base OL, O= 3x, L = 2x + 15, D = 4x + 30, LM = 4x. Find each angle.
11 Lesson Questions: Part I Find the measure of each angle. 1. mR 2. mP Find each value. 3. x y 5. x
12 Lesson Questions: Part II 6. An obtuse angle of an isosceles triangle measures (a + 15)°, and one of the primary angles measures 7a°. Find the measure of each angle. Classifying Triangles by Angles and Sides: Sliding Problems with Angle Sides in Triangle ABC BC<CA<AB. List the angles from smallest to largest.
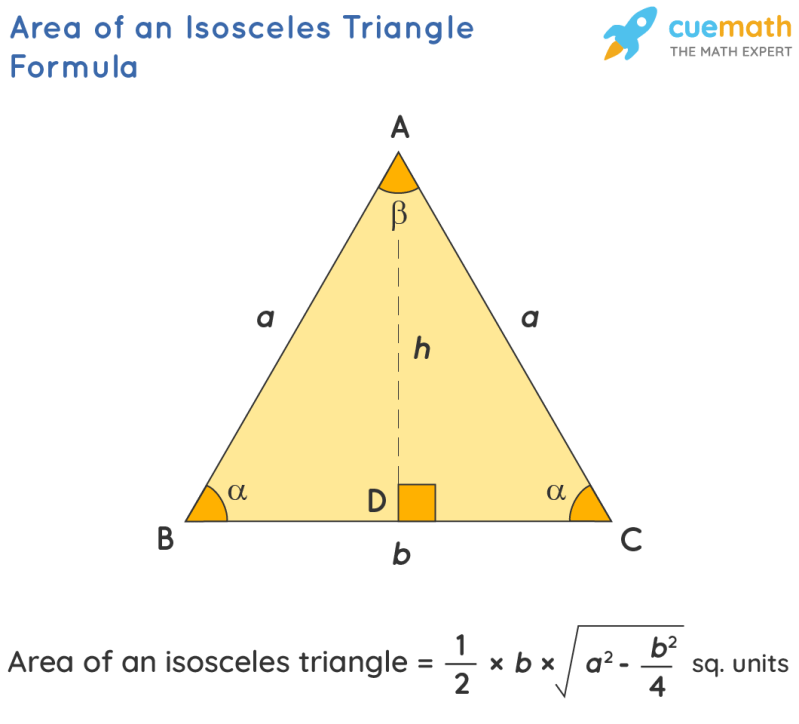
Area Of Isosceles Triangle
To operate this website, we record user data and share it with processors. To use this website, you must agree to our privacy policy, including our cookie policy. ematics Stack Exchange is a question and answer site for people of all education levels and professionals in related fields. . It only takes a minute to sign up.
Find the measure of the vertex angle $alpha$ of an isosceles triangle with a given area $A$ so that the radius $r$ of the circle inscribed in the triangle is maximal.
The equation becomes $$a+b-c=a+c-b=b+c-a$$ or $$a=b=c, $$ which says that $r$ gets its maximum value, when our triangle is an equilateral triangle,
Theorem 1: All triangles in a given frame have equal area. Theorem 2: The radius of the radius $r$ for a triangle $triangle ABC$ is given by $r = 2 frac $
Prove: If A Line Containing A Vertex Of An Isosceles Triangle Is Parallel To The Base Of The
According to Theorem 2, if we have two such triangles, one of which has the smaller perimeter, we obtain a larger circle of radius $r$.
Let $cal T$ be any triangle with area $A$ and assume that it is not equilateral. According to Theorem 1, an equilateral triangle with the same perimeters has the largest area. We can measure this equilateral triangle as a triangle $cal E$ where $Area(cal E) = A$ and $Perimeter(cal E) < Perimeter(cal T)$.
If you draw a piece from the center of the circle to each vertex, cut the triangle into 3 smaller triangles. Since the sides of the beam are perpendicular, all 3 triangles have height $r$. Let $b$ be the length of the adjacent side $alpha$. Then the area of 2 triangles is $br/2$. The length of the opposite side of $alpha$ is $2bsin(alpha/2)$ so the area of the third triangle is $brsin(alpha/2)$. The total area is then
So now we “just” maximize $r$. This is a computational mess. Get $r$ relative to $alpha$. Set the waste to zero and get $pi/3$. But I did the last part with maple. It looks like the hand of a very patient person.
Solved:write A Two Column Proof. The Median To The Base Of An Isosceles Triangle Bisects The Vertex Angle
As a guide, https://en.wikipedia.org/wiki/Incircle_and_excircles_of_a_triangle#Incircle_and_its_radius_properties has a section with an answer to this question. For the rest of the question, I use $alpha$ to be $frac$ for readability.
Now, we consider the area in terms of the radius of the circle. You can find better details on the Wikipedia page, but we will transform the triangle into three smaller triangles by drawing lines from their edges to the center of the circle. Since the circle is tangent to each edge, we know that the radius joining the center to each edge is at right angles to the edge, and consequently the altitude of each of these three subtriangles.
. Therefore, the total area is $$A = sum_ A_ = (frac + frac + frac) = frac(2a + 2a*sin(alpha))$$

You must be logged in to answer this question. Not the answer you’re looking for? Browse other questions tagged calculusgeometryinequalitytrianglesmaximum-minima.
Lesson 4 6 Isosceles Triangles.
By clicking “I accept all cookies”, you agree that StackExchange may store cookies on your device and disclose information in accordance with our Cookie Policy. Isosceles triangles are triangles that have at least two equal sides. We know that triangles are closed polygons with three sides and are classified as equilateral, isosceles and scalenes based on the length of their sides. In this article, we will learn about the definition of an isosceles triangle and its properties.
An isosceles triangle is a triangle with two sides of equal length. Let’s do a little activity to understand it better. Take a rectangular sheet of paper and fold it in half. Draw a line from the folded top edge to the bottom edge (as shown in the figure below). You can see a triangle when you open the sheet. Mark the vertices of the triangle as O, D, and C. Now measure OD and OC. Repeat this activity with different steps and observe the pattern. We can see that OD and OC are always equal. This type of triangle where two sides are equal is called an isosceles triangle.
In the figure above, △ODC is an isosceles triangle with OD = OC and ∠ODC = ∠OCD. Let us now know some properties of isosceles triangles in the next section.
Each geometric shape has certain characteristics that make it different and unique from others. Here is a list of some properties of isosceles triangles:
Solved] C Is The Incenter Of Isosceles Triangle Abd With Vertex Angle Abd….
Like any other triangle, an isosceles triangle has three angles that add up to 180 degrees. Of the three interior angles, the angles other than the apex angle are equal in measure. The isosceles triangle theorem states that the opposite angles of an isosceles triangle are equal in measure. So, in an isosceles triangle △ABC where AB = AC, we have ∠B = ∠C.
If the measure of equal angles is each less than 45 degrees, then the acute angle will be an obtuse angle. If each equal angle measures 45 degrees, then the upper angle is a right angle. And, if each equal angle measures more than 45 degrees and less than 90 degrees, the angle above will be an acute angle.
The three most common types of triangles are scalene, congruent, and isosceles triangles. Each triangle differs from the other based on its unique characteristics. A scalene triangle is one in which all three sides and three angles are of equal measure, an equilateral triangle is one in which all three sides and angles are equal, and in an isosceles triangle, two sides and two angles are equal as measure. Refer to the table below to understand the differences and similarities between scalene, equilateral and isosceles triangles.

The vertical bisector of the upper angle divides that angle and the unequal side of the triangle.
Isosceles & Equilateral Triangles Problems (video)
A triangle in which at least two sides are equal is called an isosceles triangle. Following this, if two sides of a triangle are equal, then the opposite angles of those sides are also equal.
The isosceles triangle theorem states that when two sides are equal, the base angles are also equal. The isosceles triangle theorem is also true, which states that if two angles in a triangle are equal, then the opposite sides of those angles are also equal.
A triangle can be isosceles, isosceles, or equilateral when classified by the length of its sides. In a triangle, if any two sides are of equal length, it is considered an isosceles triangle.
In an isosceles triangle, two angles are equal in measure. These angles are opposite to equal sides. When all three angles are equal, it is known as an equilateral triangle.
The Vertex Angle Of An Isosceles Triangle Is 41°. Each Of The Legs Measures 32 Centimeters. How Long
An isosceles triangle has one vertical angle and two base angles. The base angles of an isosceles triangle measure the same.
In an isosceles right triangle, equal sides form right angles. In other words, any triangle with angles of 90°, 45°, 45° is an isosceles right triangle. Includes properties of right triangles and isosceles triangles.
Yes, isosceles triangles can be right triangles if their three angles are 90°, 45°, and 45°. In an isosceles right triangle, the equal sides meet to form a right angle, and the hypotenuse is the unequal side.

)], where a is the length of the equal side and b is the base of the triangle. When the base and height/altitude of the triangle are given, then the isosceles can be found using the area of the triangle.
Isosceles Triangles ( Read )
Base angle of an isosceles triangle, isosceles triangle angle measures, the vertex angle of an isosceles triangle, vertex angle of an isosceles right triangle, isosceles triangle right angle, isosceles triangle angle formula, vertex angle of an isosceles triangle definition, what is the vertex angle of an isosceles triangle, isosceles triangle angle rules, vertex of an isosceles triangle, isosceles triangle angle calculator, vertical angle of an isosceles triangle
