Triangular Prism Vertices Edges Faces – A prism is a three-dimensional object that has two identical and equal shapes. The same shape is called the base. A base can have a polygonal shape such as a triangle, square, rectangle, or pentagon. The figure below shows three prisms.
A prism is a member of the polyhedron family with two identical and parallel bases. The base is connected crosswise to the flat face.
Triangular Prism Vertices Edges Faces

Generally, a prism refers to a transparent material used to reflect or disperse a beam of white light. It is a commonly used tool in physics.
Biaugmented Triangular Prism
Depending on the base, the prism can be of different shapes. Some common shapes are: triangle, rectangle, square, pentagon, hexagon, heptagon, octagon, and trapezoidal. For example, a triangular prism has three bases and a square prism has one square base, here are some additional figures:
A prism can be classified as regular or irregular according to its cross-sectional consistency. It can be right or oblique depending on the competition of its roots.
Volume = Base Area × Height, where, the height is the distance between the 2 bases or the length of the prism.
Find the area of a triangular prism whose base area is 12 cm 2 , perimeter 16 cm and length 7 cm.
D Shapes Worksheets
Total Surface Area (TSA) = (2 × Base Area) + (Perimeter × Height), where base area = 12 cm
Find the total and external area of an angle whose base is 36 cm 2 , perimeter 30 cm and altitude 11 cm.
Total Surface Area (TSA) = (2 × Base Area) + (Perimeter × Height), Base Area = 36 cm

Find the volume of a triangular prism whose base area is 64 cm2 and height is 7 cm. Learn about the definition of a polyhedron, about prisms and pyramids as types of polyhedra, and about a polyhedron and its net relationships. After attempting the questions, click on the buttons to see the answers and explanations in text or video.
Recognizing Common 3d Shapes (video)
A. Determine the number of polygons needed to fill your polyhedron. List the polygons and how many of them are needed.
B. Organize the cut out into a net, tape it and fold it, which can be assembled into a polyhedron. Sketch the net. If possible, find more than one way to align the polygons (show a different net for the same polyhedron).
A polyhedron is a triangle with faces. Each face is a full-in polygon and meets only one face at an entire edge. The ends of edges meet at points called vertices.
A prism is a type of polyhedron with two identical faces that are parallel to each other and called a base. The base is connected by a set of rectangles (or sometimes parallelograms).
D Shape Object Posters
A prism is named for the shape of its base. For example, if the base is a pentagon, it is called a “pentagonal prism”.
A pyramid is a type of polyhedron that has a distinct face called a base. All other faces are triangles meeting at a vertex.
The pyramid is named for the shape of its base. For example, if the base is a pentagon, it is called a “pentagonal pyramid”.

A net is a representation of two sides of a polyhedron. It is made up of polygons that form the face of a polyhedron.
D Shapes Interactive Exercise For Functional Skills
In a cube, each face shares its edges with 4 other squares. In a cubic net, not all edges of the squares coincide with other edges. When the net is folded, each of these open edges joins another edge.
Each side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.
A prism is a type of polyhedron that has two bases that are duplicates of each other. Bases are connected with rectangles or parallelograms.
Volume And Surface Area Of A Prism (video)
A pyramid is a type of polyhedron with one base. All other faces are triangles, and they all meet at a vertex.
3. Tyler said that this net does not net a square prism because all faces are not square.
5. One. A parallelogram has a length of 12 meters and a height of 1.5 meters. What is its area?

B. A triangle has a base of 16 inches and a height of ⅛ inch. What is its area?
How Many Faces And Edges Does A Triangular Prism Have?
C. A parallelogram has an area of 28 square feet and a height of 4 feet. What is its basis?
D. A triangle has an area of 32 square millimeters and a base of 8 millimeters. How tall is he?
Try the free Mathway calculator and solutions below to practice more math. Try the examples provided or type your own problem and check your answer with step-by-step explanations.
We welcome your suggestions, comments and questions about this site or page. Please send your feedback or questions on our feedback page. The area to the right of a triangular prism is the area obtained by calculating the area of its face. In a right triangular prism, the three rectangles are congruent. Also, the top and bottom two base triangles are parallel and congruent. A rectangular face or outer face is perpendicular to the base of the triangle. Now that we understand the shape of a right triangular prism, let us see what is the area of a right triangular prism.
Prisms Fun With By D. Fisher
The lateral area of a right triangular prism is the number of square units that fit inside it. A right triangular prism is a polyhedron with polygons as its faces. It has 6 vertices, 5 faces and 9 edges. Of the 5 faces, the triangle forms the top and base and the rectangle forms the outer/vertical face. The lateral area of a right triangular prism is also known as the lateral surface of the triangular prism. The unit of lateral area of a right triangular prism is given in square units, which is m
The 2-D net of a right triangular prism looks like a combination of 2 triangles and 3 rectangles. So, 2 triangles and 3 rectangles come together to form a right triangular prism.
The lateral area of a right triangular prism is equal to the area of the vertical face of the right triangular prism. Since the rectangles are perpendicular, to find the area of the right side of the triangular prism, we can find the area of each rectangle and then add them.

⇒ LA = 3lb where, l is the length of the rectangle, and b is the width of the rectangle.
Education Resources For Teachers, Schools & Students
Example: Find the area of the right side of a triangular prism whose triangular faces are 6 units long and 3 units wide.
If you engage in rote learning, you will forget the material. Plus, you’ll learn to see and marvel at the results.
The lateral area of a right triangular prism is defined as the number of square units that fit in the right triangular prism. A right triangular prism has three equal rectangles. Also, the top and bottom two base triangles are parallel and congruent. A rectangular face or outer face is perpendicular to the base of the triangle.
The formula for the external area of a right triangular prism is given as LA = 3lb, where l is the length of the rectangle and b is the width of the rectangle. The shape of the area on the right side of a triangular prism shows the direct dependence of the area on its face.
Learn About Different Sections Of Solids. 3d Shapes, Nets
How to find the length of a rectangular face if the lateral area of a right triangular prism is known?
How to find the surface area of a right triangular prism if its total area is known?
Steps to determine the area of the right side of a triangular prism if the total surface area is known:

What happens to the lateral area of a right triangular prism if the length and width of one face are tripled?
List Of 3d Shapes Name And Pictures For Kids » Onlymyenglish
Lateral area of a right triangular prism is 9 times its original value “l” and “b” are replaced by “3l” and “3b” in the formula for lateral area of a right triangular prism A = 3lb. = A = 3 × (3l) × (3b) = 9 (3lb) which gives 9 times the original value of the external area.
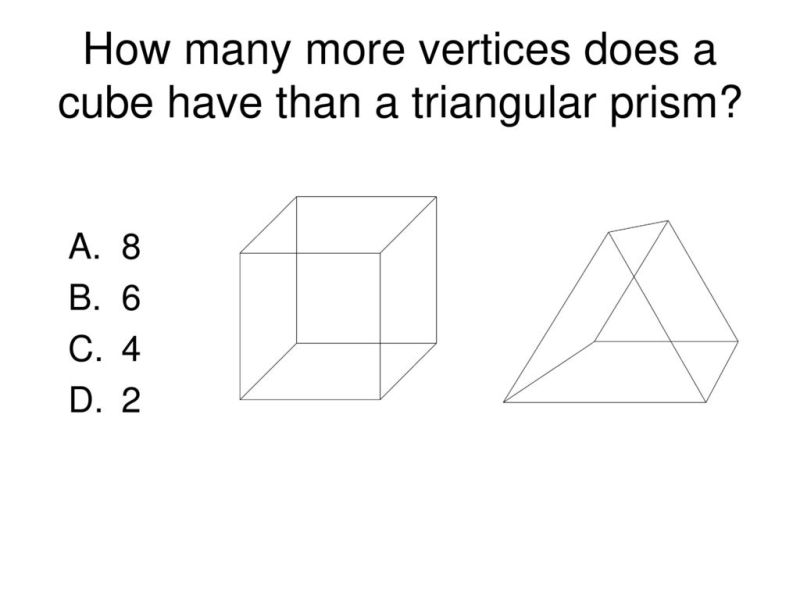
How many faces edges and vertices in a triangular prism, rectangular prism faces edges vertices, prism faces edges vertices, hexagonal prism faces edges vertices, triangular prism faces edges and vertices, a triangular prism has how many faces edges and vertices, triangular prism faces edges vertices, faces edges and vertices of triangular prism, triangular pyramid faces edges and vertices, triangular pyramid faces edges vertices, 3d shapes rectangular prism faces edges vertices, triangular prism has how many faces edges and vertices