How Many Rectangular Faces Does A Triangular Prism Have – A prism is a three-dimensional solid object with two equal and parallel faces facing each other. Similar shapes are called bases Bases can be any polygonal shape such as triangle, square, rectangle or pentagon. The diagram below shows a triangular prism
A prism is a member of the family of polyhedra consisting of two equal and parallel polygonal bases. The bases are connected by flat faces forming a uniform cross-section
How Many Rectangular Faces Does A Triangular Prism Have

In general, a prism refers to a transparent solid that is used to refract or disperse a beam of white light. It is a widely used tool in physics
Solved The Diagram Below Is Of A Triangular Prism That Has
A prism can have different shapes depending on the base Some common shapes are: triangular, rectangular, square, pentagonal, hexagonal, octagonal, octagonal, and trapezoidal. For example, a triangular prism has a triangular base and a square prism has a square base, here are some other shapes:
A prism can also be classified as regular or irregular based on the uniformity of its cross section. It can be straight or skewed depending on the alignment of its bases
Volume = Base Area × Height, where height is 2 the base or length of the prism
Find the surface area of a triangular prism whose base area is 12 cm2, perimeter 16 cm and length 7 cm.
Counting Faces And Edges Of 3d Shapes (video)
Total surface area (TSA) = (2 × base area) + (perimeter × height), where base area = 12 cm.
Find the total and lateral surface area of a rectangular prism whose base area is 36 cm2, perimeter 30 cm and height 11 cm.
Total surface area (TSA) = (2 × base area) + (perimeter × height), where base area = 36 cm.

Find the volume of a triangular prism whose base area is 64 cm2 and whose height is 7 cm. The lateral area of a right triangular prism is the area obtained by adding the areas of its lateral faces. In a right triangular prism, the three right sides are equal Also, the bases of the upper and lower triangles are parallel and congruent to each other The rectangular or lateral faces are perpendicular to the triangular base Based on our understanding of the shape of a right triangular prism, let us know what is the lateral area of a right triangular prism.
Finding The Surface Area Of Right Angled And Isosceles Triangular Prisms
The lateral area of a right triangular prism is the number of unit squares that can fit into it A right triangular prism is a polyhedron with a polygon as its face It has 5 vertices, 2 faces and 9 edges Out of the 5 faces, the triangle forms the top and base and the rectangle forms the side/vertical face The lateral area of a right triangular prism is also called the lateral surface area of a triangular prism. The units of lateral area of a right triangular prism are given in square units, i.e. m
The 2D mesh of a right triangular prism looks like a combination of 2 triangles and 3 rectangles. So, 3 triangles and 3 rectangles join to form a right triangular prism.
The lateral area of a right triangular prism is equal to the area of the vertical face of the right triangular prism. Since rectangles form vertical sides, to find the lateral area of a right triangular prism, we can find the area of each individual rectangle and then add them.
⇒ LA = 3 lb Where, l is the length of the rectangle and b is the width of the rectangle
How Does The Surface Area Definition Apply To 3d Objects?
Example: Find the lateral area of a right triangular prism that has a triangular face that is 6 units long and 3 units wide.
By engaging in rote learning you are likely to forget concepts Plus, you’ll learn visually and be amazed by the results
The lateral area of a right triangular prism is defined as the number of unit squares that can fit into a right triangular prism. A right-angled triangular prism has three right-angled sides that are equal Also, the bases of the upper and lower triangles are parallel and congruent to each other The rectangular or lateral faces are perpendicular to the triangular base
The formula for the lateral area of a right triangular prism is given as LA = 3 lb, where l is the length of the rectangle and b is the width of the rectangle. The formula for the lateral area of a right-angled triangular prism shows the direct dependence of a right-angled face on it.
Rectangular Prism Black And White Stock Photos & Images
How to find the length of a rectangle if the lateral area of a right triangular prism is known?
How to find the lateral area of a right triangular prism if its total surface area is known?
The steps to determine how to find the lateral area of a right triangular prism if the total surface area is known are:
What will be the lateral area of a right triangular prism if the length and width of a right-angled face are tripled?
Equilateral Prism, 2
The lateral area of a right triangular prism becomes 9 times its original value as “l” and “b” are replaced by “3l” and “3b” in the lateral formula of a right triangular prism as A = 3lb = A. = 3 × (3l) × (3b) = 9 (3lb) which gives 9 times the original value of the lateral area. This article is about the geometry of the pyramid For the pyramid-shaped structure, see Pyramid For other uses, see Pyramid (disambiguation).
) is a polyhedron formed by connecting a polygonal base and a point, called a vertex. Each base and vertex form a triangle, called a side It is an angular solid with a versatile base A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-sustaining
A right pyramid has its base directly above its base angle A non-right pyramid is called an oblique pyramid A regular pyramid has a regular polygon base and is usually referred to as a right pyramid.

When not specified, a pyramid is generally assumed to be a regular square pyramid, similar to natural pyramidal structures. A pyramid based on a triangle is usually called a tetradron
Solved] Marco Has Drawn A Line To Represent The Perpendicular Cross Section…
Among oblique pyramids, such as acute and obtuse triangles, a pyramid can be said to be acute if its apex is inside the base, and obtuse if its apex is outside the base. A rectangular pyramid has its top on top of an edge or base In a tetrahedron this criterion varies depending on which face is considered the base.
Pyramids are a class of prisms The pyramid can be doubled by adding a second offset point on the other side of the base plane
Or [1, n], with 2n sequences An extended Schläfli symbol ( ) ∨ , representing a point, ( ), added (orthogonal displacement) to a regular polygon, can be given. A join operation creates a new edge between all pairs of two pairs of shapes
A triangular or triangular pyramid with all equilateral triangular faces becomes a regular tetrahedron, one of the Platonic solids. A lower symmetric case of triangular pyramids is C|
Solved A Triangular Prism Lands On One Of Its Three
, which has an equilateral triangle base and 3 equal isosceles triangle sides. Square and pentagonal pyramids can also be formed by regular convex polygons, in which case they are Johnson solids.
If all the edges of a square pyramid (or any convex polyhedron) are tangent to a sphere such that the average location of the points of contact is on the circumference of the sphere, then the pyramid is said to be regular and forms half of it. Regular estradiol
A hexagon or pyramid with a high base must be formed by isosceles triangles. A hexagonal pyramid with equilateral triangles will be a perfectly planar shape, and a hexagon or an equilateral triangle will not meet at all.

A right pyramid can be labeled as ( ) ∨P, where ( ) is the vertex, ∨ is a union operator, and P is a base polygon.
What Are The Similarities And Differences Between A Prism And A Pyramid?
An orthogonal tetrahedron isosceles triangle can be written as ( ) ∨ [ ( ) ∨] as the union of a point with the base of an isosceles triangle, as ( ( ) ∨ ( )] ∨ or as the union (orthogonal displacement) of two orthogonal segmts, a diagonal bisphere. , contains 4 isosceles triangle faces. It has C.
The volume of a pyramid (even any angle) is V = 1 3 b h}bh}, where b is the area of the base and h is the height from the base to the top. It works for any polygon, regular or irregular, and for any vertex position, if measured as the vertical distance from the plane containing the base. In 499 AD Aryabhata, the mathematician-astronomer from the classical era of Indian mathematics and Indian astronomy, used this method in the Aryabhatia (Section 2.6).
The same equation, V = 1 3 b h}bh}, also applies to angles with any base. This can be proved by the same argument as above Look up the volume of a cone
For example, the volume of a pyramid whose base is an n-sided regular polygon of side length and whose height is
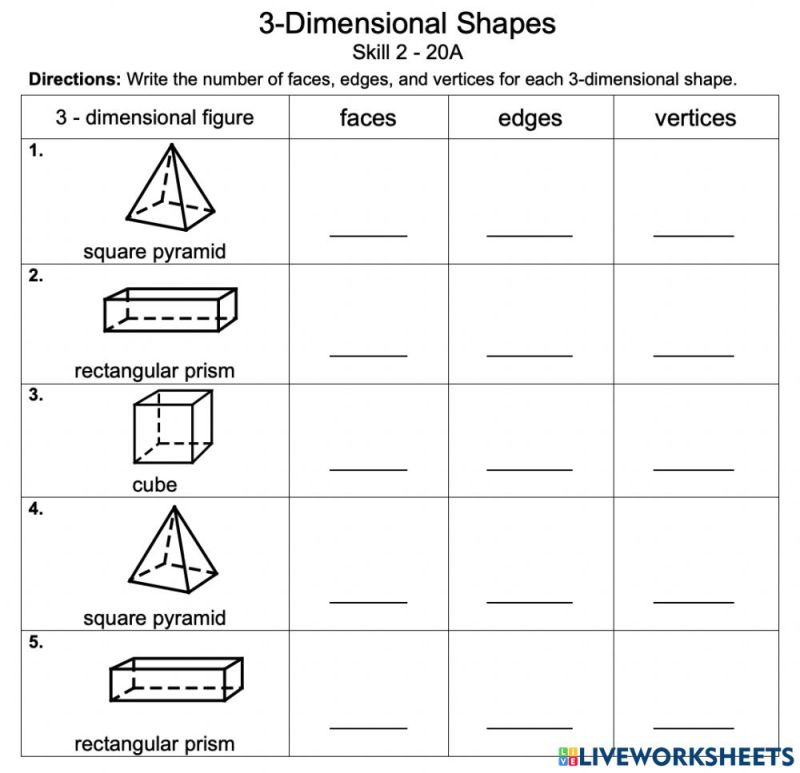
Faces, Edges, Vertices Worksheet
Triangular prism faces, a rectangular prism has how many faces, how many faces does triangular prism have, rectangular triangular prism, how many faces a triangular prism have, how many faces triangular prism have, how many faces has a triangular prism, rectangular prism has how many faces, how many faces rectangular prism have, how many rectangular faces does a triangular prism have, how many faces does a triangular prism, how many faces vertices edges does a triangular prism have
