Capital Letters With Rotational Symmetry – Rotational Symmetry: A geometric shape or object is said to be symmetrical if it is divided into two or more identical pieces and arranged in an orderly manner. The property of rotational symmetry is that a shape looks the same after partial or complete rotation.
The degree of rotational symmetry is the number of possible orientations in which an object appears the same for each complete rotation. In this article, we will discuss symmetry especially rotational symmetry, real life examples and line symmetry.
Capital Letters With Rotational Symmetry

Symmetry is a term used in the study of geometry, derived from a Greek phrase that means measuring together. The two objects must be the same size and shape must be symmetrical, except that one object is oriented differently than the other. A single object, such as a figure, can have symmetry.
The Order Of Rotational Symmetry Of A Square Is (a) 1(b) 2(c) 3(d) 4
According to the mathematical definition “Symmetry is a mirror image.” Symmetrical images, shapes or objects are similar to each other.
A line of symmetry is a line that completely divides a shape into two parts. If you fold a shape along a line of symmetry, both sides of the object or shape match exactly. The curvature of a line does not change if a mirror is placed around it.
An axis of symmetry is a line that divides or cuts a figure or object into two equal parts. An axis of symmetry is also called a line of symmetry. A line of symmetry divides a shape or object into two halves that mirror each other.
In the illustration below, the material star is bent along a line of symmetry. Each segment on either side of a line of symmetry is the same.
The Number Of Capital Letters Of The English Alphabets Having Both Horizontal And Vertical Lines Of Symmetry Are
1. Line of Vertical Symmetry: A line of vertical symmetry separates or cuts the object, shape or image into two equal parts below or above. A vertical line of symmetry separates or cuts the shape in two directions: down and up.
Example: Cut the bottom shape vertically down as shown. On the left and right sides of a line of symmetry, the units of form are the same. As a result, a line of symmetry is formed.
2. Horizontal line: When you divide or cut any item or shape horizontally, the units produced are the same from left to right or right to left. They are called figures of symmetry, and the line of symmetry is called a horizontal line.

Example: As an example cut the shape below horizontally from left to right. The shape elements above and below the line of symmetry are the same.
Plzzzz Help!! Copy The Venn Diagram At Right Onto Your Paper, Then Carefully Place Each Capitalized
3. Diagonal line of symmetry: it is formed when we divide or cut an object or shape into two identical parts on the diagonal. An object is cut diagonally by a diagonal line of symmetry.
Example: When this object is divided diagonally, both sides of the diagonal (line of symmetry) are mirror images of each other. A diagonal line of symmetry is the name given to a line of symmetry.
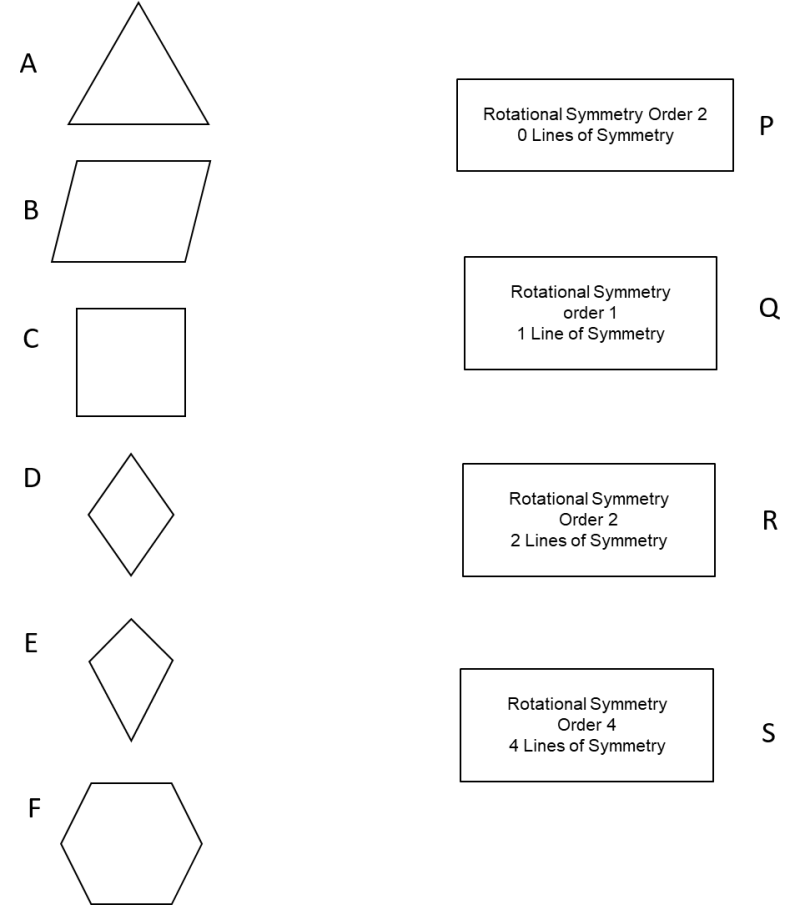
Lines of Symmetry: Multiple lines of symmetry can be found in shapes or patterns, the number of times they can be folded in half and still look the same on both sides.
Rotational Symmetry: When a shape or pattern rotates or revolves around a central point, it is said to have rotational symmetry. A shape can be said to have rotational symmetry of order (X) if it can be rotated around the center point (X) while remaining the same.
New Electronics Symbol Sticker Pack! #ios #imessage « Adafruit Industries
Since a regular pentagon has five equal sides and five lines of symmetry, its order of rotational symmetry is five. Due to its rotational symmetry, the pentagon can rotate (5) times before returning to its initial position. Every time it rotates, it looks the same as the original position.
A rotation is a transformation that causes a preimage face to rotate or flip to the location of the image face. Everything else rotates around a fixed point called the center of rotation of all rotations.
This point can be inside the figure, in which case the figure remains fixed and only rotates. Alternatively, the point may be outside the figure, causing the figure to move.

The number of times you can rotate a geometric object to make it look like the original shape is called its order of rotational symmetry.
Solved] For Each Capital Letter In The English Language In This Font: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Count The Number Of Proper…
In the English alphabet, rotational symmetry refers to the fact that a letter retains its appearance after being rotated. The letters (}) and (Z) are capital letters with rotational symmetry.
Answer: A square is a quadrilateral with linear and rotational symmetry of order greater than (1.)
When a shape or pattern rotates or twists around a central point, it is said to have rotational symmetry. A line of symmetry is a line that divides a shape exactly in half. If you fold a shape along a line of symmetry, both sides of the object or shape match exactly. This article includes explanations of symmetry, line symmetry, rotational symmetry, order of rotational symmetry, angle of rotation, etc.
This helps in better understanding of rotational symmetry. The result of this paper helps in solving various problems based on rotational symmetry.
Solved 3. Which Capital Letters Of Our Alphabet Have The
Answer: Rotational symmetry of a shape describes how the shape of an object remains even when it is rotated on its axis.
Q.2. What is the order of symmetry of rotation of a square? Answer: (4) is a square order of rotational symmetry.
Q.5. Which image has reflection rotation and point symmetry? Answer: A point of symmetry says that each side has a corresponding side, the same distance from the center point but in opposite directions. From the figure, circle only follows reflection, rotation and point symmetry.

Q.6. What is a line of symmetry? Answer: A line of symmetry is a line that cuts a shape exactly. If you fold a shape along a line of symmetry, both sides of the object or shape match exactly. The curve of a line does not change if a mirror is placed on it. Like this book? You can publish your book online for free in minutes! Create your own flipbook
Using Letters Of The Alphabet
Explanation: Geometry Lab Section 5 Symmetry 71 5. Organize the capital letters into the following two lists: those that have rotational symmetry and those that do not. Rotational Symmetry:
5 Symmetry Many of the activities in this section present opportunities for students to express themselves mathematically and artistically—you will be able to create many bulletin board displays from the work done in the various labs. Perhaps you should plan to put together a final performance based on the best work in this section. (See the Teacher’s Notes to Lab 5.5 for ideas about demonstrating symmetry.) Note that the first lab is a prerequisite for all the others. An excellent resource on symmetry mathematics and crystallographic notation for symmetric patterns is Handbook of Regular Patterns: Peter S. Introduction to Symmetry in Two Dimensions by Stevens. In addition to a clear presentation of ideas, the book contains thousands of symmetrical images from every culture on the planet. Another good reference on symmetry is Martin Gardner’s Ambidextrous Universe. It opens with the question, “Why do mirrors flip left and right, but not up and down?” See page 191 for teacher notes for this section. Geometry Lab Section 5 Symmetry 69 © 1999 Henry Picciotto, www.MathEducationPage.org LAB 5.1 Name(s) Introduction to Symmetry 1. The following are lines of symmetry: a. These letters are not: a. Explain the difference. B. Draw a line or a line of symmetry on each letter in the first group. (In some cases, there are two lines.)2. Show how the five capital letters not shown in Problem 1 can be written in two ways: symmetrical lines, or not. 3. Arrange the lowercase letters in the following two lists: symmetrical lines, and not. Line of Symmetry: Not Line of Symmetry: 4. Some figures have rotational symmetry and some figures do not. Explain the difference.has rotational symmetry. Organize the capital letters into the following two lists: those with rotational symmetry and those without. Rotational symmetry: No rotational symmetry: 6. Organize the lowercase letters into the following two lists: those with rotational symmetry and those without. Rotational Symmetry:No Rotational Symmetry:7. Artist Scott Kim finds ingenious ways to fit letters into symmetrical word designs. Explain the symmetry of the design below. From Homosexuality, Scott Kim.8. On a separate sheet of paper, write the terms of symmetry. In this context, symmetry can be interpreted in many ways, using uppercase or lowercase letters. This list provides possible definitions. A. Words with a horizontal line like COB. B. Words with a vertical line of symmetry like TOT. (To make it easier, you can write the words vertically, with each letter below the previous letter.) c. Word pairs that are mirror images of each other, such as box and pax (use a horizontal mirror). D. Words that can be read upside down like SOS. E. couples
Objects with rotational symmetry, logos with rotational symmetry, which letters have rotational symmetry, letters with symmetry, words with rotational symmetry, capital letters of the alphabet with rotational symmetry, 4 capital letters with rotational symmetry, what letters have rotational symmetry, letters with rotational symmetry, shapes with rotational symmetry, capital letters with lines of symmetry, which letters of the alphabet have rotational symmetry