How Many Faces Does A Polygon Have – Geometrically, a neahedron (or nonahedron) is a polyhedron with nine faces. There are 2606 types of convex Neahedrons, with different types of vertices, edges and connecting faces.
The most common neahedra are octagonal pyramids and heptagonal prisms. The heptagonal roof is like a polyhedron, with two regular heptagon faces and sev square faces. An octagonal pyramid has eight isosceles triangular faces around a regular triangular base. Two other nehdra were also found in Johnson’s solids: the long square cone and the lateral cone. A triquetral associahedron, with six pentagonal faces and three square faces, is a neahedron. The five Johnson solids have double neahedra: a triangular dome, a gyrolong square pyramid, a double square pyramid, a double triangular prism, a triangular prism (both of which are associahedrons), and a triangular icosahedron. Another neahedron is a reduced trapezoid with a square base, and 4 kites and 4 triangular faces.
How Many Faces Does A Polygon Have

The Herschel graph shows the edges and edges of the Herschel neahedron above, with all its square faces. It is the simplest polyhedron without a Hamiltonian cycle, the only neahedron in which all faces have the same number of vertices, and one of the three nehedra with two dimensions.
Polygons And Solids
Cutting the rhombic dodecahedron along the diameters of the four faces in the middle results in a dual neahedron, a reduced trapezohedron, one square face, four faces of a rhombus, and four faces of an isosceles triangle. Like the rhombic dodecahedron itself, this shape can be used to describe three-dimensional space.
A long version of this style can still be seen in space at the top of the rear tower of the 12th century Romanesque Basilica of Saint Mary (Maastricht). The towers themselves have four corners, four roof faces and a square base, another space that fills the neahedron.
2606 There are topologically convex neahedra, mirror images excluded. These can be divided into 8, 74, 296, 633, 768, 558, 219, 50, with 7 to 14 columns respectively.
A chart of these figures, with a detailed description of the nine-pointed nehdra, was first published by Thomas Kirkman in the 1870s. Learning a new word every day is a great habit to adopt. (I’m sure Mr. Garfield thinks so). In that spirit, here’s an interesting math term you might not be aware of: “Dodecahedron”. What is it? I’m glad you asked. Here are 12 things you need to know.
What Shape Has 9 Edges, 6 Vertices, And 5 Faces?
Both triangles and squares are two squares, two-dimensional figures formed by straight lines. Just to kick things off, let’s go add a third reason. A polyhedron is a 3-D object composed of several faces. Therefore, while a square is a polyhedron, a cuboid is a polyhedron. Remember that at your next wine and cheese party (“Hey, do I have more of these cheddar polyhedra here?”).
As you will know if you have ever been to Washington D.C. pentagons are 2-D shapes with five straight sides forming a pentagon. Dodecahedrons (pronounced dow·deh·kuh·he·druhns) are three-dimensional bodies with twelve flat faces—all shaped like a pentagon.
Time to make dad smile at the “Big Fat Greek Wedding”. “Dodecahedron” comes from the Greek words “dodeca” and “ivy”, that is 12 and “seat or base”.

“Spirits” are not mental; are lines where two sides of polygons (triangles, triangles, etc.) meet in a polyhedron. Vertices or “vertices” are small points where three or more faces meet. Any dodecahedron with identical faces will have 30 vertices and 20 vertices.
Geometric Solids And Surface Area
Check your mood at the door. A polyhedron is considered regular if all its faces are congruent; (b) All angles fit; and the extremes are equal in length. Mathematicians have proved that there are only five types of polyhedra. Together they are known as five “Platonists”. And the regular dodecahedron becomes one of them.
Cubes (otherwise: “regular hexahedra”) are the most famous of the Platonic solids, he reports. You also know tetrahedrons, pyramids with triangular bases. Next is the octahedron, a species of eighty faces, which is like a diamond. Finally, there is an icosahedron with 20 – count em, 20 – triangular faces.
Here’s a cool trick: If you connect five tetrahedra and use the shape of the corners to create many new faces, you’ll just have a perfect dodecahedron. In the same way, there are many ways of combining cubics using the base dodecades. Spatial shenanigans are a lot of fun.
If you lived in a giant dodecahedron, how would you get from point A to point B? It’s actually easier than you think to install. In 2018, mathematicians Jayadev Arthrea, David Aulicino and Pat Hooper showed that it is possible to draw a straight line in a dodecahedron that starts from one vertex and returns to the same point without turning or crossing other vertices. However, this cannot be done in any way with a cube, tetrahedron, octahedron or icosahedron.
How Many Vertices Does A Rhombus Have?
Since 1739, archaeologists have excavated dozens of small tombs in areas occupied by the Roman Empire. Generally, the bronze ones, which are hollow, have spheres at the corners, and each face has a round hole in the middle. The examples found so far were built between the years 1 and 500 CE. Opinions differ on the role; We all know that small things are weapons, anklets, candles, or anything else.
Braarudosphaera bigelowii was a type of algae that lived during the time of the Dinosaurs. Our organism is found in geological sites around the world, arranged in two-dimensional scales like a dodecahedron. Too bad we never found a dinosaur with such a wild body and design.
Participants die in many shapes and sizes in this fantasy role-playing game. D12 rifles, a tool in many situations involving large weapons, are mini-dozens.

Since Christ had twelve disciples and there are several months in the year, Dali felt that the “12 pentagons of the dodecahedron” were appropriate (thematically) for the actual painting he completed in 1955.
D Building Model Simplification Method Considering Both Model Mesh And Building Structure
Special Offers on Anti-Virus Software from HowStuffWorks and TotalAV Security Try Our Crossword Puzzle! Can you solve these puzzles? A polyhedron is a 3D shape with flat faces, straight edges, and sharp edges. “Polyhedron” comes from the Greek word, where “poly” means many, and hedron means “above”, so when many equal parts are joined, they form a polyhedron. These shapes are named after faces which are usually polygonal. The most common names are cubes, hexagons, etc. Let’s learn more about the types of polyhedra and solve a few examples to better understand the shape.
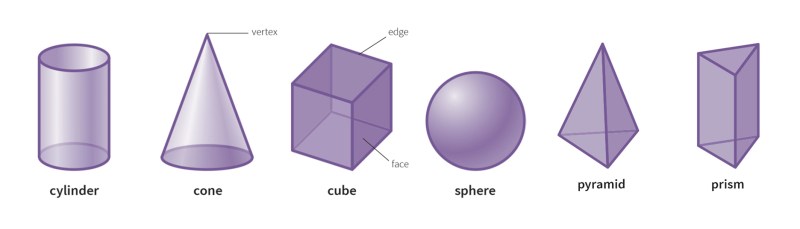
A polyhedron is a three-dimensional solid made of polygons. It has a flat face, straight edges, and straight edges. For example, a cube, prism, or pyramid are polyhedra. Cones, spheres, and cylinders are not polyhedrons because their sides are not polygons and they have curved surfaces. The plural polyhedron is also called polyhedra. They are classified as prisms, pyramids and platonic solids. For example, a triangular prism, a square prism, a rectangular pyramid, a square pyramid, and a cube (the Platonic solid) are polyhedra. Look at the following diagram, which shows the different types of polyhedra.
A regular polyhedron is also called a Platonic solid whose faces are regular polygons. In a regular polyhedron, all polyhedral angles are equal. There are five regular polyhedra. The following is a list of five common polyhedra.
A polyhedron that has many faces that are not contiguous, and whose angles are not equal, is called an irregular polyhedron.
Blend Of 2 Pentagrammic Prisms
A convex polyhedron is similar to a polygon. If the line segment joining two points on the surface of the polyhedron lies entirely within the polyhedron, it is called a convex polyhedron.
A concave polyhedron floor is very similar to a polygon. If a line segment joining two points on the surface of the polyhedron leaves the polyhedron, it is called a concave polyhedron.
There is a relationship between the number of faces, edges and angles in a polyhedron. We can represent this relationship in a mathematical form called Euler’s Formula.

Euler’s formula ⇒ F + V – E = 2, where, F = number of faces, V = number of vertices, E = number of edges.
Three Dimensional Shapes
Using Euler’s formula we can easily find the missing part of the polyhedron. We can also find out whether a polyhedron with a given number of segments exists or not. For example, a cube has 6 faces, 8 edges (corner points) and 12 corners. Let us check whether the cube is a polyhedron or not using Euler’s formula. F = 6, V = 8, E = 12
E. formula ⇒ F + V – E = 2 where, F = number of faces; V = number of vertices; E = number of angles
Substituting formula values: 6 + 8 – 12 = 2 2 = 2. Obviously, the cube.
How many faces does a octagonal prism have, how many faces does triangular prism have, how many angles does a polygon have, how many faces does a dodecahedron have, how many faces does a diamond have, how many faces does the moon have, how many faces does a cone have, how many faces does a polygon have, how many sides does a polygon have, how many edges does a polygon have, how many faces cube have, how many faces does a triangular pyramid have