Quadrilateral With 4 Congruent Sides – By definition, opposite sides are parallel. Other Properties: Opposite sides are congruent. Opposite angles are congruent. The following angles are complementary. Diagonals intersect in half.

A rectangle is a quadrilateral with _______________. Four right angles are rectangular parallelograms? Yes, because opposite angles are congruent. Thus, a rectangle has all the properties of a parallelogram. Opposite sides are parallel and congruent. Opposite angles are congruent. The following angles are complementary. Diagonals intersect each other.

Quadrilateral With 4 Congruent Sides

Theorem: If a parallelogram is a rectangle, then its diagonals are congruent. Therefore, ∆AEB, ∆BEC, ∆CED and ∆AED are isosceles triangles. E D C B A Inverse: If the hypotenuses of a parallelogram are congruent, then the parallelogram is a rectangle.

Ways To Find The Area Of A Quadrilateral

If AC = 21, then BE = _________. If m < 1 = 4x and m < 4 = 2x, find x. If m < 2 = 40, find m < 1, m < 3, m < 4, m < 5, and m < 6. x = 9 pcs 10.5 pcs x = 18 pcs 6 5 4 3 2 1 E D C B A m <1 = 50O, m <3 = 40O, m <4 = 80O, m <5 = 100O, m <6 = 40O

A rhombus is a quadrilateral with four congruent sides. Is a rhombus a parallelogram? ≡ Yes, because the opposite sides are convergent. ≡ Therefore… the opposite sides are parallel and congruent. Opposite angles are congruent. The following angles are complementary. Diagonals intersect each other.

Theorem: The diagonals of a rhombus are right angles. Theorem: Each diagonal of a diamond intersects opposite angles. Note: Small triangles are correct and useful!

10 Examples of rhombus….. Data: ABCD is a rhombus. Complete the following. If AB = 9 then AD = ______. If m <1 = 65, m <2 = _____. m < 3 = ______. If m <ADC = 80, m <DAB = ______. If m <1 = 3x -7 and m <2 = 2x +3, then x = _____. 9 units 65° 90° 100° 10

Quadrilaterals (sample Questions)

11 Definition of Square: A square is a quadrilateral with four congruent angles and four congruent sides. Is a square a parallelogram? Yes, because both opposite sides and opposite angles are congruent. It is also a rectangle and a rhombus. Therefore… the opposite sides are parallel and congruent. Opposite angles are congruent. The following angles are complementary. Diagonals intersect each other. Plus: The diagonals are congruent and perpendicular. Diagonals cross opposite corners.

12 Squares – Examples … … Data: ABCD is a square. Complete the following. If AB = 10 then AD = _______ and DC = _______. If CE = 5 then DE = _______. m <ABC = _____. m < ACD = _____. m <AED = _____. 10 units 10 units 5 units 90 ° 45 ° 90 °

A quadrilateral with exactly one pair of opposite parallel sides. Parallel sides are called bases, and non-parallel sides are called legs. It is complemented by successive angles between the bases. Trapezoidal Leg Base Leg Base

The middle section of the trapezoid is the section that joins the midpoints of the legs. Theorem – The median of a trapezoid is parallel to the base. Theorem – The length of the median is half the sum of the lengths of the bases. middle segment

Classifying Quadrilaterals #1 Quiz

RSTV trapezoidal signal with RS and TV bases. RS_____ TV If mTSR = 75o, mSTV = ________ Find the center of ST and label it B. Find the center of RV and label it C. Join B and C to form ____________. BC is parallel to ____________. If RS = 8 and TV = 12 then BC = ___. R S C B 105o V T Middle segment RS and TV 10

1. Both pairs of base angles of an isosceles trapezoid are congruent. 2. The diagonals of an isosceles trapezoid are congruent. B. A. D. C

Find the missing values. 4x -5 6x – 9 J M K L 3y – 5 7 + y JL = 4x – 2 MK = 3x + 8 57 y x x = 57o 4x – 5 = 6x – 9 – 5 = 2x – 9 57 + y = 18 4 = 2x y = 123o 2 = x

21 Kite Definition: A square with two distinct pairs of continuous congruent sides. Note: Opposite sides are not compatible! Assertion: The diagonals of a kite are perpendicular. Theorem: Exactly one pair of opposite angles are congruent. Note: Congruent angles are formed by incongruent adjacent sides. A pair of non-congruent opposite angles is intersected by a diagonal.

Quadrilaterals And Their Properties Diagram

In order for this website to work, we record your data and share it with processors. To use this website, you must agree to our Privacy Policy, including our Cookie Policy. These words are used all the time by teachers and we are used to hearing them, but what do they really mean and how can we tell the difference between these special quadrants?

Together, we will test our knowledge and discover the amazing properties of these three special parallelograms.

First, note that rectangles, squares, and rhombuses (plural of diamonds) are quadrilaterals that have all the properties of parallelograms.

The biggest distinguishing features are their four sides and four corners. A rectangle is a parallelogram with four right angles. A rhombus, sometimes called a rhombus or a diamond, as the math nicely states, is a parallelogram with four congruent sides. A square is a parallelogram with four right angles and four congruent sides.

A Four Sided Figure Opposite Sides Parallel And Congruent Opposite

A: In the case of a diamond, we guarantee that all sides are the same length, while a parallelogram only specifies that opposite sides are congruent.

A: A square and a rhombus have four congruent sides, but a square also has four congruent right angles, while a rhombus only specifies that the opposite angle is congruent and does not have to be 90 degrees.

A: A square is a rectangle because it fulfills all the properties of a rectangle. Remember that for a parallelogram to be a rectangle, it must have four right angles, opposite sides congruent, opposite sides congruent, opposite congruent angles, diagonals bisect each other, and diagonals congruent. A square meets all these requirements, so a square is always a rectangle.

A: A diamond can only be a rectangle if all four corners of the diamond are 90 degrees.

Congruent Shapes: Triangles, Quadrilaterals, Irregular Shapes And Circles • 7esl

Together, we will look at various examples in which we will use our properties of rectangles, diamonds, and squares, as well as our knowledge of the relationship of pairs of angles, to determine missing angles and side lengths.

Additionally, we will use our understanding of isosceles, isosceles, and right-angled triangles to find the indicated measure and perimeter of a given polygon. A rectangle is a parallelogram with four right angles. | | A square is a parallelogram with four congruent sides and four right angles.

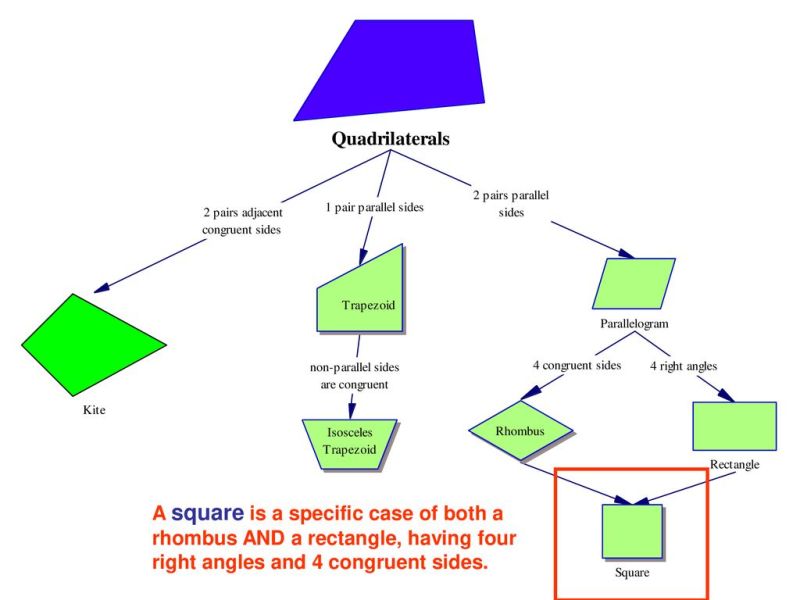
A Venn diagram shows the relationship between parallelogram, rhombus, rectangle and square. Each shape has properties for each group to which it belongs. For example, a square is a rectangle, a rhombus, and a parallelogram, so it has all the properties of each of these shapes.

Describing a special parallelogram Determine whether the statement is always, sometimes, or never true. A rhombus is a rectangle. Help. Solution This statement is sometimes true. In a Venn diagram, the diamond and rectangle regions overlap. If a rhombus is a square, then it is a rectangle.

Parallelogram Congruent Sides

Describing a special parallelogram Determine whether the statement is always, sometimes, or never true. A parallelogram is a rectangle. Help. Solution This statement is sometimes true. Some parallelograms are rectangles. In a Venn diagram, you can see that some shapes in the area of ​​the parallelogram are in the area of ​​the rectangle, but many are not.

A rectangle using special properties of parallelogram ABCD. What else do you know about ABCD? Solution A B D C Since ABCD is a rectangle, it has four right angles by definition. The definition also states that a rectangle is a parallelogram, so ABCD has all the properties of a parallelogram: 1 Opposite sides are parallel and congruent. 2 opposite angles are congruent and subsequent angles are supplementary. 3 diagonals intersect each other.

A rectangle using special properties of parallelogram ABCD. What else do you know about ABCD? A B D C A A rectangle is defined as a parallelogram with four right angles. But every quadrilateral with four right angles is a rectangle because every quadrilateral with four right angles is a parallelogram.

Special Quadrilateral Factor Rhombus Factor A quadrilateral is a rhombus if and only if it has four congruent sides. A factored rectangular quadrilateral is a rectangle if and only if it has four right angles. A square factor quadrilateral is a square if and only if it is a rhombus and a rectangle. You can use this conclusion to prove that the quadrilateral is a rhombus, rectangle, or square without first proving that the quadrilateral is a parallelogram.

Geometry Quadrilaterals Chart Diagram

In the figure, PQRS is a diamond. What is the value of y? 2y + 3 5y – 6 P Q R S Solution All four sides of the rhombus are congruent, so RS = PS. 5y – 6 = 2y + 3 equal lengths of congruent sides. 5 years = 2 years + 9 add 6 years each

Quadrilateral with two pairs of congruent sides, area of quadrilateral given 4 sides, a quadrilateral with four congruent sides, area of quadrilateral with 4 different sides, a quadrilateral with opposite sides that are parallel and congruent, quadrilateral with all sides congruent, quadrilateral with congruent sides, quadrilateral with congruent diagonals, area of a quadrilateral given 4 sides calculator, shapes with congruent sides, a quadrilateral with 4 congruent sides, quadrilateral with one pair of parallel sides